The methods explained in BIP’s 32, 43 & 44 are best practice for Bitcoin wallets, and necessary for interoperability with other Bitcoin wallets.
WHAT IS AN HD WALLET?
There are two types of deterministic wallets, sequential and hierarchical. Here we’ll focus on the industry standard, hierarchical.
Hierarchical deterministic wallets make managing a wallet and it’s keys dramatically easier than the JBOK’s wallets discussed in lesson 8. These wallets create a tree like structure of a master key, parent keys and children keys.
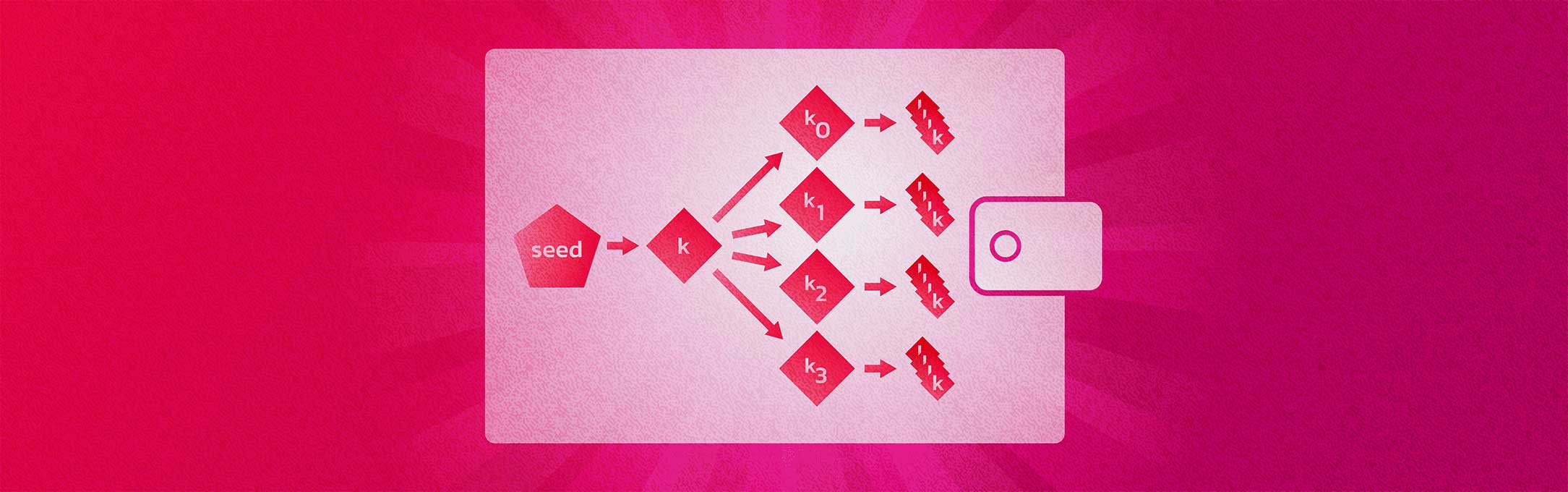
These wallets are created using a “seed” as discussed in lesson 8. This way an entire wallet, containing many addresses/key, can be migrated or restored using just the mnemonic phrase (and optionally a password). Also in lesson 8 we covered how the mnemonic seed functions. In this lesson we will focus on the functionality of HD wallets and how keys are derived from the master key.
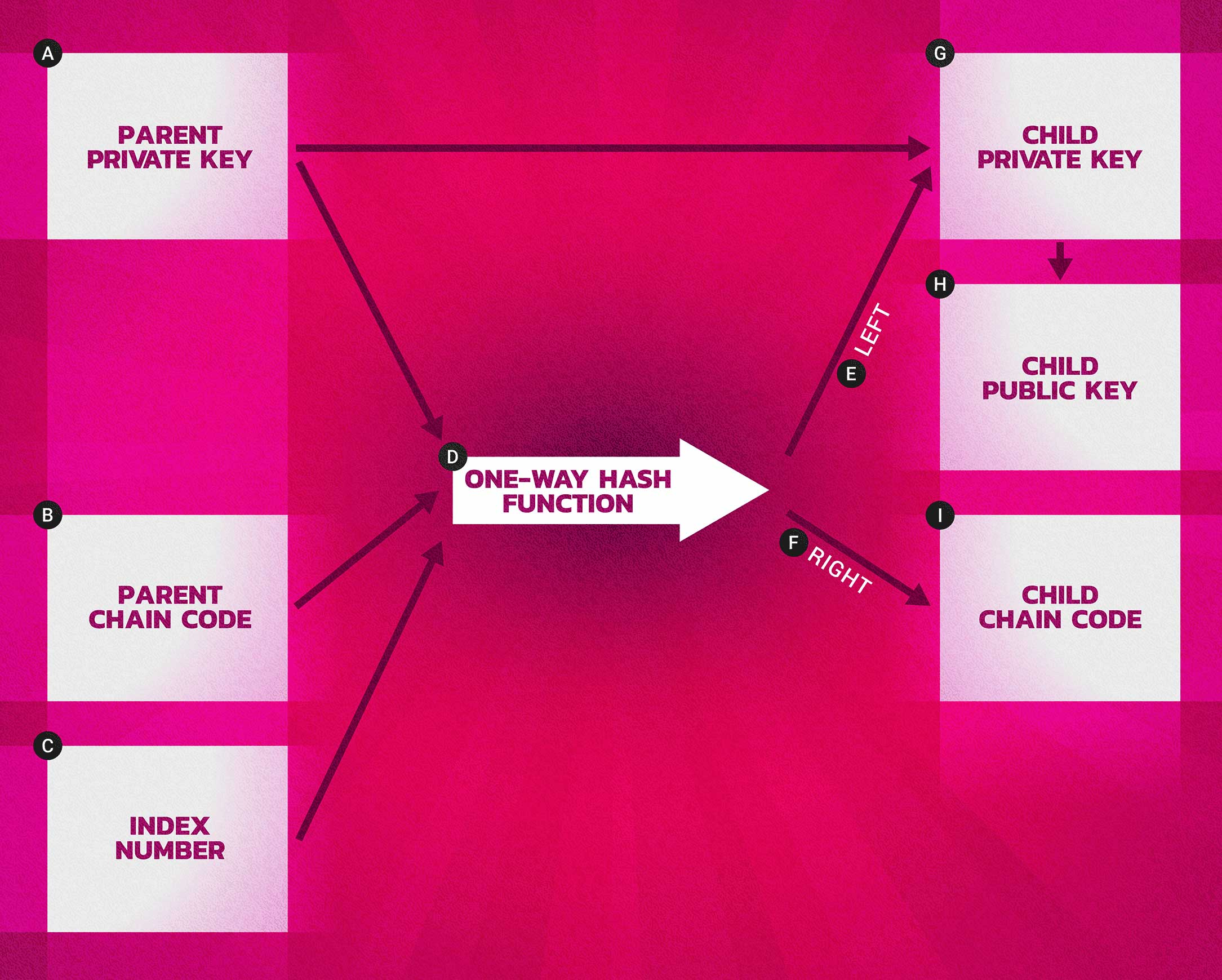
First let’s introduce this thing called a “chain code”. A chain code is 256 bits of entropy, essentially, a random number. This extra bit of of randomness makes it not possible to determine sibling keys even if one child key is known. It adds security.
The root of the chain code is derived from the wallet seed. As the wallet key tree is expanded parent chain codes are derived from the root and child chain codes are derived from parent chain codes, etc.
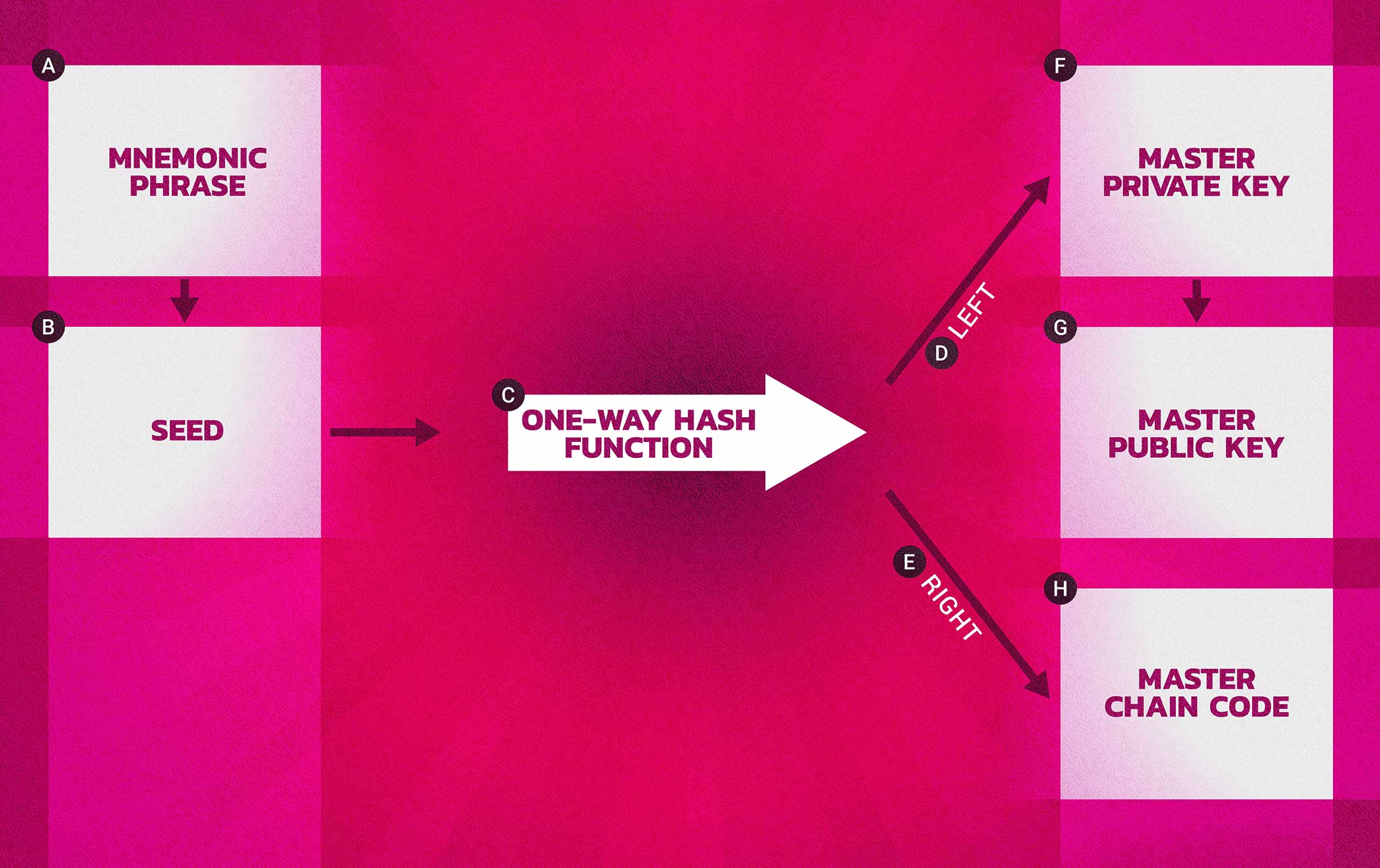
To create a wallet key tree you need the master or parent private key and corresponding public key, the root or parent chain code, and and index number (which we’ll discuss shortly). All of this is run through a hashing function and split into a child private key a corresponding public key and a child chain code.
The below image is helpful in visualizing this process.
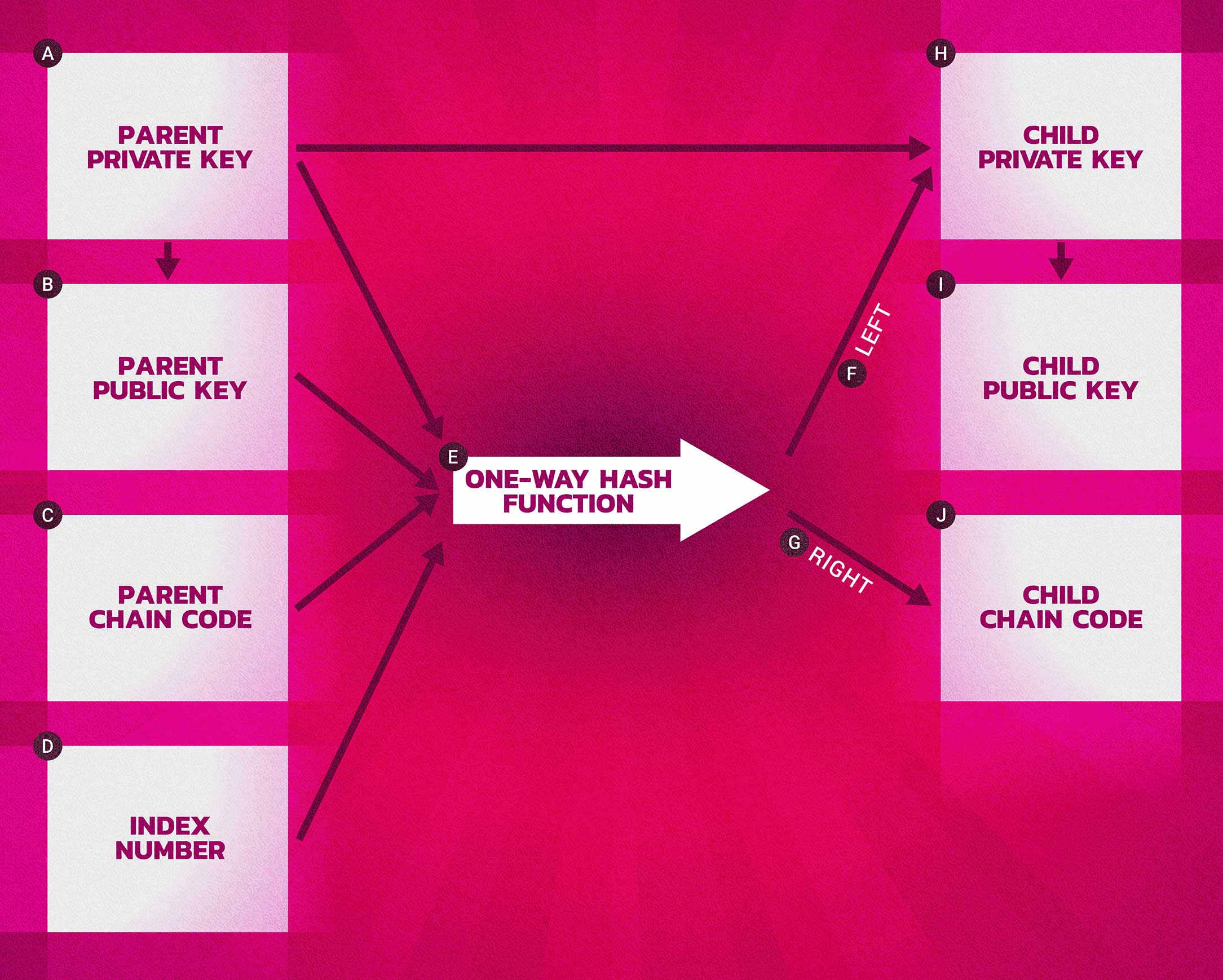
This process has some really neat features. Child keys and subsequent addresses derived in this fashion are indistinguishable from nondeterministic keys and address. They function entirely as “normal” keys. And child key can not be used to find a parent or sibling keys. You would need both the child private key and the child chain code to derive more children.
A key, public or private concatenated with the chain code is called an extended key. A key of this type is encoded using Base58Check and uses a special version number that results in the prefix “xprv” for private keys and “xpub” for public keys. While these keys are called “extended” they are extensible and can be used to generate children and entire branches of the wallet tree.
An extended public key has some very useful features. It can be placed on a public server and used to generate more public keys and addresses, that can be controlled with the wallet seed, all while the private key can remain safely offline.
This is particularly useful in an e-commerce scenario. Image an online retailer who does a lot of business in bitcoin. It is advantageous to have each order that comes in be paid to a new address. This allows the store managers to associate payment address with specific orders. Without HD wallets and public key derivation, show in the image below, private keys would have to be stored on a public server or publics keys would have to be generated before hand and preloaded on the server. However, with HD wallets, one extended public key from the wallet can be stored on the server and then used to derive new public keys and address for each new order that comes in.
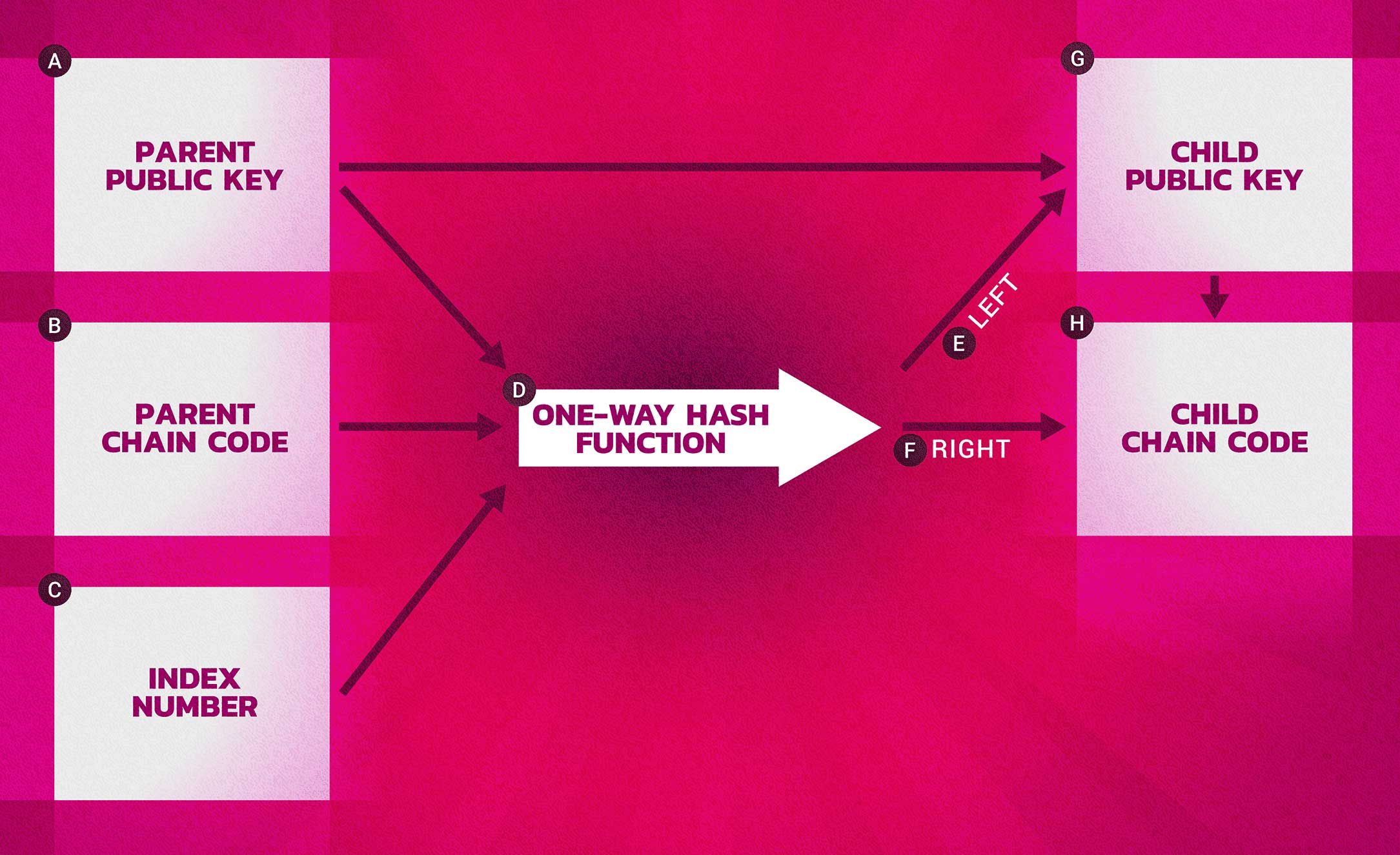
While an extended public key, or xpub, is very useful it comes with some potential risks. An xpub key contains the chain code, which, if the xpub private key were somehow also know could be used to derive all other child private keys.
A solution to this problem is a “hardened key”. This is an alternative derivation function which discontinues the relationship between the parent public key and the child chain code. This “hardened” derivation function uses the parent private key, rather than the parent public key, to derive the child chain code.
Using the hardened key derivation function the resulting child private key and chain code are completely different from what would have existed using the standard key derivation function. The new, hardened, branch of keys can be used to produce extended public keys that are not vulnerable to a chain code leak as the chain code they contain cannot be exploited to reveal any private keys.
In an e-commerce setting, it is best for any xpub keys used on the server to have been derived from a hardened parent.
In part two of Bitcoin for Developers we’ll take a deep dive into Bitcoin transactions and cover how to integrate bitcoin payments into an e-commerce shop.
INDEX AND PATH
As you may have noticed mentioned when describing key derivation, an index identifier is used.
The index is a 32-bit integer that is used to distinguish between normal vs hardened keys. The index is split into two ranges, the first portion is reserved for normal derivation and the second portion reserved for hardened derivation.
THE PATH
Keys in an HD wallet are identified using a path naming convention. Here each level of the tree is separated by a slash.

For example, private keys that are derived from the master private key start with “m” while public keys that were derived from the master public key start with “M”. These are listed in the index as m/0 or M/0. Their children keys will be shown as m/0/0 or M/0/2, etc.
Keep in mind that this path is read from right to left. So the path M/0/2 is read as the third grandchild of key M/0 which is the is the first child of the master key.
These paths are very helpful for navigating the key tree created by an HD wallet. Each parent extended key can have 4 billion children, 2 billion “normal” and 2 billion “hardened”. All of those children can have 4 billion grandchildren, etc, without any set limits.
BIPS 43 and 44 address this complexity issue with some proposed standards.
The BIP 43 standard uses the first hardened child as as an identifier of the purpose of the tree.
BIP 44 specifies a structure consisting of five predefined tree levels. Specifically, purpose, coin type, account, change and address index as illustrated below…
In the BIP 44 standard, the purpose is always set to 44. The coin type specifies which coin this branch of the wallet is for (HD wallets can be used with many cryptocurrencies with a similar structure to Bitcoin). For example Bitcoin is 0 and Litecoin is 2.
The account level allows the user to divide their wallet for organizational purposes. Perhaps one branch for different divisions of an organization.
The “change” level has two subtrees, one for creating receiving addresses and one for creating change addresses.
And lastly, the fifth level is the address index as describes as above.
So, the third child of the master public key on the Bitcoin network might look something like this… M/44/0/0/0/2.
Further reading:




